Imagine a formula that would allow you to take data from a very small pool of users (often as few as 8; possibly as few as 3) and figure out why, for instance, Autodesk customers are calling support, whether Budget.com visitors can rent a car in under a minute, or why cardholders were reluctant to use a mobile payment site.
Such a formula exists, and it’s not some abstract “formula for success” in management strategy or a design technique. We’re talking about a mathematical formula that’s easy to use but can transform the way you measure and manage the user experience.
The formula is called the Adjusted-Wald Binomial Confidence Interval (“Adjusted-Wald Interval” for short), but its name isn’t as important as what it can do. Its power is in helping estimate the behavior of an entire user population, even when the sample size is small. It does this by taking a simple proportion as input and producing a confidence interval. For example, suppose 10 users have attempted a task and 7 completed it successfully. The simple successful completion rate is 70%. But, given such a small sample size, how can you have any faith in the result? Would it be reasonable to expect to get exactly 7,000 successes if the sample size was 10,000? Probably not, but how far off might it be?
This is when you need the power of a confidence interval, which provides a range of plausible results with a specific level of statistical confidence (typically set to 95%). Working with the range rather than the observed proportion helps to protect decision makers from being fooled by randomness. For the example of 7 out of 10 users successfully completing a task, an adjusted-Wald interval set to 95% confidence ranges from about 39% to 90%. Having a range like this dramatically enhances decision making, especially if there are established benchmarks for comparison. A confidence interval that ranges from 39% to 90% is very wide—over 50 percentage points—but in addition to knowing that the most likely completion rate is around 70%, you also know that it is very unlikely that the completion rate for the population is less than 39% or greater than 90%. If there was a pre-established goal of a completion rate of at least 90%, then this design has clearly failed. On the other hand, if, based on previous designs or field data, the goal was a completion rate greater than 35% this design has clearly succeeded. If the goal was anywhere between 39% and 90%, then it’s necessary to withhold judgment and collect more data.
Sometimes it can be more valuable to think in terms of failure rates rather than success rates. Continuing with the example above, if there were 7 out of 10 successes, then there were 3 out of 10 failures. The 95% adjusted-Wald confidence interval for 3 out of 10 ranges from about 10% to 61%, so there is substantial confidence even with this small sample that the failure rate is unlikely to be lower than 10%. Thus, a key question driving the decision of whether there is a problem with the design is whether a task failure rate of 10% is acceptable. If not, then there is work to do to improve the design and drive down the minimum estimate of the failure rate.
We’ll look at a few case studies next, and, after that, we will explain some of the math behind the online calculator we have set up to make these calculations.
Five Case Studies
The following case studies show real-world applications of the Adjusted-Wald Interval to UX decision making. To check the results of these case studies, enter the data in our online calculator (focusing on the results for the Adjusted-Wald Interval).
Case study 1: Why are users getting a bizarre error message and calling support?
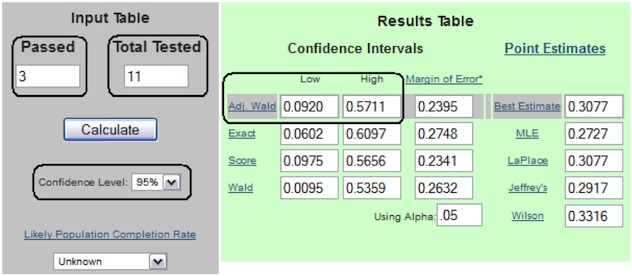
Autodesk noticed an unusually high call volume to their call center. Some users were complaining about a bizarre error message (“ADR Not Empty”) after downloading a trial version of Autodesk’s flagship product, AutoCAD. Studying the web analytics data didn’t provide any insight as to the cause of the problem. The UX team quickly set up a study in which they invited real users to share their screens as they downloaded and installed the software—11 users accepted the invitation.
Over a couple days, they watched as 3 out of 11 users (27%) selected the wrong operating system architecture (32-bit vs. 64-bit) and received that inscrutable error message. But the analytics team was concerned that such a small sample size might have yielded misleading results. To address that concern, we used the Adjusted-Wald Interval to determine that we could be 95% confident that between 9% and 57% of users would be likely to encounter the problem. Even with a small sample size, there was statistically significant evidence to conclude that a substantial portion of users (at least 9% but probably closer to 27%) would have the problem. As a result, Autodesk created a new design of the download page, which led to a substantial reduction in calls related to this issue.
Case study 2: Can users rent a car in less than 60 seconds?
The Budget Rent A Car website makes a bold promise: “Rent a car in 60 seconds.” But can a typical user really rent a car in under a minute? To find out, we had 12 people, all of whom had previously rented a car online, come to our usability lab and use the website to reserve a car. We recorded task completion times, which were (in seconds) 215, 131, 260, 171, 187, 147, 74, 170, 131, 165, 347, and 90. Only 1 person came within 14 seconds of renting a car in under a minute, so 0 out of 12 users were able to rent the car in 60 seconds. But can we really have faith in such a small sample size? The 95% confidence interval for 0/12 ranges from 0% to 22%, meaning it’s highly unlikely that even with a sample size of 10,000 we’d see more than 22% of users rent a car in under a minute. [Note: If you are a member of Budget’s loyalty program, have your personal details saved, and also knew the airport code of your destination, then you’d likely rent in under 60 seconds.]
Case study 3: Would a printed warning help users avoid mistakes in documentation?
A major computer manufacturer had discovered a critical error in the documentation for installing a new computer, and had already printed all the copies for distribution. Because it would have been expensive to reprint the installation guide, a usability study was conducted to assess the effectiveness of inserting a printed warning sheet, labeled in large type “DO THIS FIRST,” on the top of the packaging where customers would see it first upon opening the box. Despite its location and prominent label, 6 of 8 participants installing the computer ignored the warning sheet, setting it aside without attempting to use its instructions. Thus, the observed failure rate was 75%, with a 95% confidence interval ranging from 40% to 94%. The lower limit of the confidence interval indicated that it was very unlikely that the true failure rate in the population would be less than 40%. The company was unwilling to accept that level of risk, so they spent the money to update the documentation rather than relying on the warning sheet.
Case study 4: Is fear of stolen data a major inhibitor from paying a bill on a mobile website?
In a recent study of department store credit card users, we investigated why so few cardholders were using the card’s mobile payment site. We asked 16 users why they had never paid or viewed their bills on their mobile phones, and 5 out of the 16 (31%) expressed a concern over the security of their credit card and banking data over the cellular network. Using the Adjusted-Wald method, we inferred (with 95% confidence) that between 14% and 56% of all users likely felt this way. These results led the company to focus on improving security messaging and awareness since the data encryption and protection on cellular networks is as good as or better than many home networks.
Case study 5: What percent of users had problems adding GPS to their rental car?
In another rental car usability test, we asked 45 participants to find out how much it would cost to rent a car with a GPS navigation system on Enterprise.com. This time, the test wasn’t in a lab; it was a remote, unmoderated study using screen recordings of user sessions from around the U.S. We observed 33 out of 45 users (73%) having trouble adding the GPS to their reservation because this option was available only after users entered their credit card details. Based on the adjusted Wald interval, we were 95% confident that between 59% and 84% of users who wanted to add GPS to their reservation would encounter the same problem during the reservation. We suspect that a good portion of these users might think the option isn’t offered and would either rent without the option or, at even greater cost to Enterprise, decide to rent the car elsewhere.
And Now, the Math
As promised, here’s some information about the math behind the online calculator (for more details, see Chapter 3 of our book, Quantifying the User Experience: Practical Statistics for User Research). Don’t worry if this gets a little complicated—in practice just think of it as a black box, or just skip over this and move on to the conclusion.
Most research done with customers and users, such as surveys or usability tests, uses a small subset of the entire population as the sample. Although there are many ways to measure the user experience, it’s possible to measure almost anything using a simple binary metric, e.g.:
- Yes/No
- Purchase/Didn’t Purchase
- Recommended/Didn’t Recommend
- Pass/Fail
Code each outcome simply as a 1 or 0. The average of those 1s and 0s produces a proportion. To compute a confidence interval using the information in a proportion, it’s necessary to know the numerator (e.g., number of successes, x), the denominator (the sample size, n), and the desired level of statistical confidence (typically, 95%). The range around the observed proportion is the standard error times the standardized (i.e., z) score for the desired confidence level. For binary data, the standard error is the square root of p(1-p)/n, where p is the observed proportion and n is the sample size. The value of z for 95% confidence intervals is 1.96.
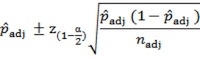
Applying this method to the observed proportion produces the well-known (to statisticians) Wald Interval, which does not produce accurate ranges when sample sizes are small. The Adjusted-Wald Interval, a recent innovation, uses adjusted values for x and n to get an adjusted value of p to use for the center of the interval and to use when computing the standard error. The specific adjustment is to add z to x and z2 to n—an adjustment that greatly increases the accuracy of the interval, even when sample sizes are very small. For 95% confidence the value of z (1.96) is close to 2, so a rule of thumb for the Adjusted-Wald adjustment is to add two successes and two failures to the observed data, making padj roughly equal to (x+2)/(n+4).
An important point to keep in mind is that the results of the adjusted-Wald interval, like all statistical methods, generalizes to the population from which the sample came. When samples are not representative of the population (a goal best assured through random sampling from the population of interest), the results will be inaccurate. The amount of inaccuracy depends on the extent to which the sample fails to represent the population, so exercise care in selecting samples. If the entire sample comes from banking customers who live in the same retirement home in Wichita, the confidence interval is valid, but is only generalizable to that limited population.
Conclusion
As our data and these examples show, you don’t always need fancy metrics or statistics to provide quantitative support for UX decisions. You can do a lot with simple binary data and this powerful formula. Keep in mind that the formula is part of a larger strategy for interpreting the data and using it to guide decision-making. You can never be sure about the accuracy of a simple proportion or percentage, but you can have a precise amount of confidence in the adjusted Wald confidence interval computed from the same data. In this way, the Adjusted-Wald Interval supports confident decision making in UX design.
Interested in learning more about quantifying the user experience and making better decisions with limited time and budgets? Join Jeff Sauro, Jim Lewis, and several other UX leaders at the Lean UX Denver conference September 19-21.
Blackboard image provided by 4freephotos.com